Gauss Jordan Elimination Method
Forward elimination of Gauss-Jordan calculator reduces matrix to row echelon form. Gauss Jordan Method Python Program With Output Gauss Jordan Method Online Calculator.
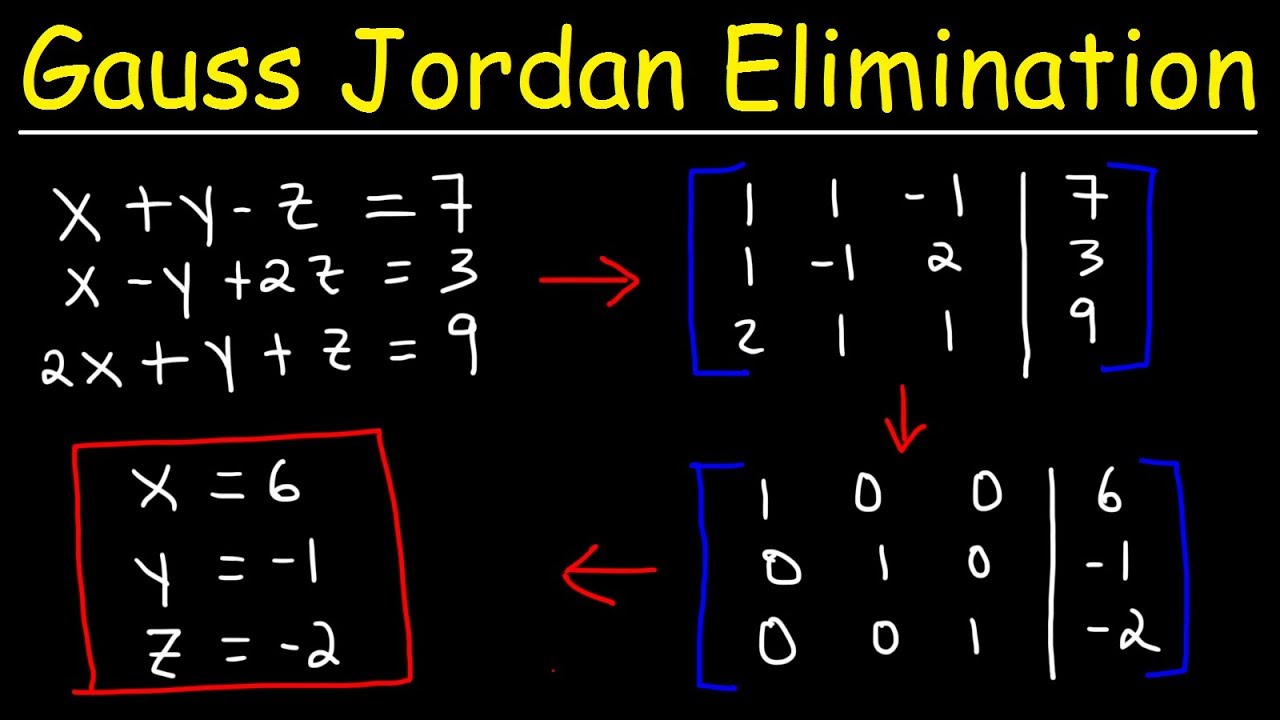
Gauss Jordan Elimination Reduced Row Echelon Form Youtube
His teacher Büttner and his assistant Martin Bartels were amazed when Gauss summed the integers from 1 to 100 instantly by spotting that the sum was 50 pairs of numbers each pair summing to 101.

. Lets see the definition first. The Gauss-Jordan Elimination method is an algorithm to solve a linear system of equations. The very first method of the Gauss Jordan Method involves the elimination of the first variable ie.
It is similar and simpler than Gauss Elimination Method as we have to perform 2 different process in Gauss Elimination Method ie. Lets recall the definition of these systems of equations. It is straightforward to program and partial pivoting can be used to control rounding errors.
Gauss Jordan Method Python Program With Output Gauss Jordan Method Online Calculator. Gauss Elimination Method Online Calculator. Set an augmented matrix.
X from all the equations except the first. Gauss Jordan Method is a little modification of the Gauss Elimination Method. Gauss Jordan Method C Program.
It was further popularized by Wilhelm Jordan who attached his name to the process by which row reduction is used to compute matrix inverses Gauss-Jordan elimination. The Gauss-Jordan method also known as Gauss-Jordan elimination method is used to solve a system of linear equations and is a modified version of Gauss Elimination Method. Set the matrix must be square and append the identity matrix of the same dimension to it.
Biography At the age of seven Carl Friedrich Gauss started elementary school and his potential was noticed almost immediately. The inverse is calculated using Gauss-Jordan elimination. Gauss elimination method is used to solve a system of linear equations.
Matrix Inverse Using Gauss Jordan. Solving systems of linear equations using Gauss Seidel method calculator - Solve simultaneous equations 2xyz53x5y2z152xy4z8 using Gauss Seidel method step-by-step online We use cookies to improve your experience on our site and to show you relevant advertising. If the calculator did not compute something or you have identified an error or you have a suggestionfeedback please write it in.
To solve a system of linear equations using Gauss-Jordan elimination you need to do the following steps. Gauss Jordan Method Pseudocode. Gauss Jordan Method Pseudocode.
We can also use it to find the inverse of an invertible matrix. Programs in any high level programming language can be written with the help of these Gauss-Seidel and Gauss Jacobi method algorithm and flowchart to solve linear simultaneous equations. We will introduce the concept of an augmented matrix.
Gauss Jordan Method Algorithm. Here during the stages of elimination the coefficients are eliminated in such a way that the systems of equations are reduced to a diagonal matrix. So this method is considered superior to the Gauss Jordan method.
This method can also be used to compute the rank of a matrix the determinant of a square matrix and the inverse of an invertible matrix. We will use the method with systems of two equations and systems of three equations. Gauss Elimination Method Python Program with Output.
Both Gauss-Jordan and Gauss elimination are somewhat similar methods the only difference is in the Gauss elimination method the matrix is reduced into an upper-triangular matrix whereas in the Gauss-Jordan method is reduced into a diagonal. This method is fast and easy compared to the direct methods such as Gauss Jordan method Gauss Elimination method Cramers rule etc. Reduce the left matrix to row echelon form using elementary row operations for the whole.
Size of the matrix. Gauss Jordan Method Algorithm. However the manual.
The Gauss Jordan Elimination or Gaussian Elimination is an algorithm to solve a system of linear equations by representing it as an augmented matrix reducing it using row operations and expressing. Gauss Elimination Method Python Program with Output. The calculator will find the inverse if it exists of the square matrix using the Gaussian elimination method or the adjugate method with steps shown.
Carl Friedrich Gauss championed the use of row reduction to the extent that it is commonly called Gaussian elimination. In the Gauss Elimination method algorithm and flowchart given below the elimination process is carried out until only one unknown remains in the last equation. Matrix Inverse Using Gauss Jordan.
Gauss Jordan Method C Program. This will allow us to use the method of Gauss-Jordan elimination to solve systems of equations. In fact Gauss-Jordan elimination algorithm is divided into forward elimination and back substitution.
To calculate inverse matrix you need to do the following steps. Gauss Jordan Method C. X y z 6 x y z 2 2x y 3z 9.
In mathematics Gaussian elimination also known as row reduction is an algorithm for solving systems of linear equationsIt consists of a sequence of operations performed on the corresponding matrix of coefficients. In this method the variables are eliminated and the system is reduced to the upper triangular matrix from which the unknowns are found by back substitution. In this section we will look at another method for solving systems.
Example Find the Solution of following Linear Equations using the Gauss Elimination Method. Gauss Jordan Method C Program. In 1788 Gauss began his.
Gauss Elimination Method Online Calculator. Gauss Jordan Method C Program.

Definition Of Gauss Jordan Elimination Method Chegg Com
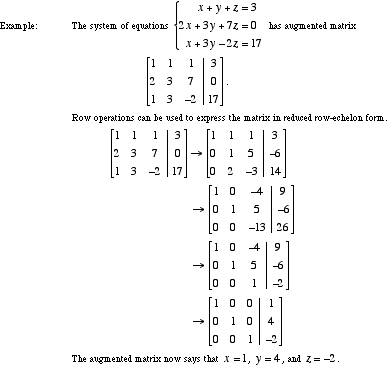
Mathwords Gauss Jordan Elimination

Gauss Jordan Elimination Reduced Row Echelon Form Youtube

Gauss Jordan Elimination Reduced Row Echelon Form Rref Youtube
No comments for "Gauss Jordan Elimination Method"
Post a Comment